Ще зі шкільного курсу алгебри та геометрії ми знаємо про поняття тривимірного простору. Якщо розібратися, сам термін «тривимірний простір» визначається як система координат з трьома вимірами (це знають всі). По суті, описати будь-об’ємний об’єкт можна за допомогою довжини, ширини і висоти в класичному розумінні. Однак давайте, як кажуть, копнемо трохи глибше.
Що таке тривимірне простір
Як вже стало ясно, розуміння тривимірного простору і об’єктів, здатних існувати всередині нього, визначається трьома основними поняттями. Правда, у випадку з точкою це саме три значення, а у випадку з прямими, кривими, ламаними лініями або об’ємними об’єктами відповідних координат може бути більше.

В даному випадку все залежить саме від типу об’єкта і застосовуваної системи координат. Сьогодні найбільш поширеною (класичної) вважається Декартова система, яку іноді ще називають прямокутною. Вона і деякі інші різновиди будуть розглянуті дещо пізніше.
Крім усього іншого, тут треба розмежовувати абстрактні поняття (якщо можна так сказати, безформні) начебто точок, прямих або площин і фігури, які мають кінцевими розмірами або навіть об’ємом. Для кожного з таких визначень існують і свої рівняння, що описують їх можливе положення у тривимірному просторі. Але зараз не про це.
Поняття точки в тривимірному просторі
Для початку визначимося, що являє собою точка в тривимірному просторі. Загалом-то, її можна назвати якоюсь основною одиницею, яка визначає будь-яку плоску або об’ємну фігуру, пряму, відрізок, вектор, площина і т. д.

Сама ж точка характеризується трьома основними координатами. Для них в прямокутній системі застосовуються спеціальні напрямні, називаються осями X, Y і Z, причому перші дві осі служать для вираження горизонтального положення об’єкта, а третя відноситься до вертикального завданням координат. Природно, для зручності вираження положення об’єкта відносно нульових координат в системі прийняті позитивні і негативні значення. Проте сьогодні можна знайти і інші системи.
Різновиди систем координат
Як вже говорилося, прямокутна система координат, створена Декартом, сьогодні є основною. Тим не менше в деяких методиках завдання місцезнаходження об’єкта у тривимірному просторі застосовуються і деякі інші різновиди.

Найбільш відомими вважаються циліндрична та сферична системи. Відмінність від класичної полягає в тому, що при завданні тих же трьох величин, що визначають місце розташування точки в тривимірному просторі, одне із значень є кутовим. Іншими словами, в таких системах використовується окружність, відповідна куті в 360 градусів. Звідси і специфічне завдання координат, що включає такі елементи, як радіус, кут і утворює. Координати в тривимірному просторі (системі) такого типу підпорядковуються іншим закономірностям. Їх завдання в даному випадку контролюється правилом правої руки: якщо поєднати великий і вказівний палець з осями X і Y, відповідно, інші пальці у вигнутому положенні вкажуть на напрям осі Z.
Поняття прямої у тривимірному просторі
Тепер кілька слів про те, що являє собою пряма в тривимірному просторі. Виходячи з основного поняття прямої, це якась нескінченна лінія, проведена через точку або дві, не рахуючи безлічі точок, розташованих у послідовності, не змінює пряме проходження лінії через них.
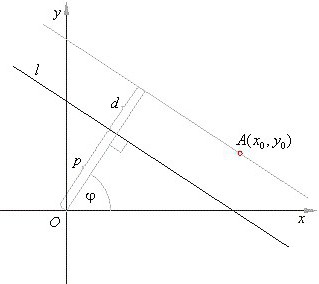
Якщо подивитися на пряму, проведену через дві точки в тривимірному просторі, доведеться враховувати по три координати обох точок. Те ж саме відноситься до відрізкам і векторах. Останні визначають базис тривимірного простору і його розмірність.
Визначення векторів і базис тривимірного простору
Як прийнято вважати, у тривимірній системі координат може існувати три основних вектори, які визначають базис. При цьому базисів з відповідними незалежними трьома векторами може бути незліченна безліч.
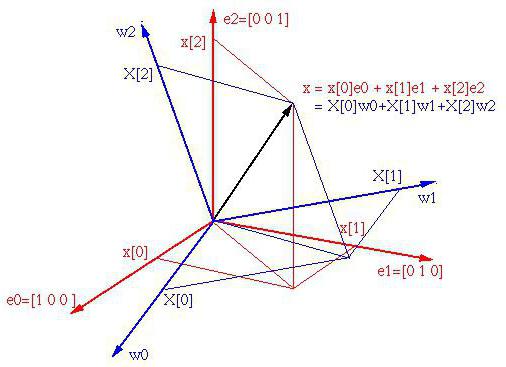
Зауважте, це можуть бути тільки три вектори, але ось трійок векторів можна визначити скільки завгодно. Розмірність простору визначається кількістю лінійно-незалежних векторів (в нашому випадку – три). І простір, в якому є кінцеве число таких векторів, називається конечномерным.
Залежні і незалежні вектори
Що стосується визначення залежних і незалежних векторів, лінійно-незалежними прийнято вважати вектори, які є проекціями (наприклад, вектори осі X, спроектовані на вісь Y).

Як вже зрозуміло, будь-четвертий вектор є залежним (теорія лінійних просторів). А от три незалежних вектора у тривимірному просторі в обов’язковому порядку не повинні лежати в одній площині. Крім того, якщо визначати незалежні вектори в тривимірному просторі, вони не можуть бути, так би мовити, один продовженням іншого. Як вже зрозуміло, що в розглянутому нами випадку з трьома вимірами, згідно загальної теорії, можна побудувати тільки трійки лінійно-незалежних векторів у певній системі координат (без різниці, якого типу).
Площини в тривимірному просторі
Якщо розглядати поняття площині, не вдаючись у математичні визначення, для більш простого розуміння цього терміна, такий об’єкт можна розглядати виключно як двовимірний. Іншими словами, це нескінченна сукупність точок, у яких одна з координат є постійною (константою).

Приміром, площиною можна назвати будь-яку кількість точок з різними координатами по осях X і Y, але однаковими координатами по осі Z. У будь-якому випадку одна з тривимірних координат залишається незмінною. Проте це, так би мовити, загальний випадок. У деяких ситуаціях тривимірний простір може перетинатися площиною по всіх осях.
Існує більше трьох вимірювань
Питання про те, скільки може існувати вимірювань, досить цікавий. Як вважається, ми живемо у тривимірному з класичної точки зору просторі, а в чотиривимірному. Крім відомих всім довжини, ширини і висоти, такий простір включає в себе ще й час існування об’єкта, причому час і простір між собою взаємопов’язані досить сильно. Це довів ще Ейнштейн у своїй теорії відносності, хоча це більше відноситься до фізики, ніж до алгебри та геометрії.

Цікавий і той факт, що сьогодні вчені вже довели існування як мінімум дванадцяти вимірювань. Звичайно, зрозуміти, що вони собою представляють, зможе далеко не кожен, оскільки це відноситься скоріше до якоїсь абстрактної області, яка знаходиться за межами людського сприйняття світу. Тим не менше факт залишається фактом. І не дарма ж багато антропологи та історики стверджують, що наші пращури могли мати якісь специфічні розвинені органи чуття зразок третього ока, які допомагали сприймати багатовимірну дійсність, а не виключно тривимірне простір.
До речі, сьогодні існує досить багато думок з приводу того, що екстрасенсорика теж є одним з проявів сприйняття багатовимірного світу, і тому можна знайти достатньо багато підтверджень.
Зауважте, що сучасними базовими рівняннями і теоремами описати багатовимірні простору, що відрізняються від нашого чотиривимірного світу, теж не завжди представляється можливим. Так і наука в цій області відноситься скоріше до області теорій і припущень, ніж до того, що можна відчути або, так би мовити, помацати або побачити на власні очі. Тим не менш непрямі докази існування багатовимірних світів, в яких може існувати чотири і більше вимірів, сьогодні ні в кого не викликають сумнівів.
Висновок
В цілому ж, ми дуже коротко розглянули основні поняття, що відносяться до тривимірного простору і базовим визначенням. Природно, існує безліч приватних випадків, пов’язаних з різними системами координат. До того ж ми постаралися особливо не лізти в математичні нетрі для пояснення основних термінів тільки для того, щоб питання, пов’язане з ними, був зрозумілий будь-якому школяру (так сказати, пояснення «на пальцях»).
Тим не менше, думається, навіть з таких простих трактувань можна зробити висновок про математичному аспекті всіх складових, що входять в базовий шкільний курс алгебри і геометрії.






