Математика – шкільний предмет, який вивчається усіма, незалежно від профілю класу. Однак вона не всіма улюблена. Часом незаслужено. Ця наука постійно підкидає учням завдання, які дозволяють їхньому мозку розвиватися. Математика відмінно справляється з тим, щоб не дати розумовим можливостям дітей згаснути. Особливо добре з цим справляється один з її розділів – геометрія.
Кожна з тим, що в ній вивчаються, гідна уваги і поваги. Геометрія – це спосіб розвинути просторову уяву. Прикладом може служити тема про площі фігур, зокрема ромбів. Ці задачки можуть завести в глухий кут, якщо не розібратися в деталях. Тому що можливі різні підходи до пошуку відповіді. Комусь простіше запам’ятати різні варіанти формул, які написані нижче, а хтось здатний сам їх отримати з раніше засвоєного матеріалу. У будь-якому випадку безвихідних ситуацій не буває. Якщо трохи подумати, то рішення обов’язково знайдеться.

Що таке ромб і чим він схожий на інші чотирикутники?
Відповісти на це питання потрібно, щоб зрозуміти принципи отримання формул і хід міркування в задачах. Адже щоб розібратися в тому, як знайти площу ромба, потрібно чітко розуміти, що це за фігура і які її властивості.
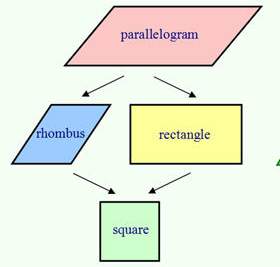
Для зручності розглянемо паралелограм, який є чотирикутником з попарно паралельними сторонами, приймемо за “батька”. У нього є двоє дітей”: квадрат і ромб. Обидва вони є параллелограммами. Якщо продовжувати паралелі, то це – “прізвище”. Отже, для того щоб знайти площу ромба, можна скористатися вже вивченою формулою для паралелограма.
Але, як і всі діти, ромб має і щось своє. Це трохи відрізняє його від “батька” і дозволяє розглядати як окрему фігуру. Адже прямокутник не ромб. Повертаючись до паралелей – вони як брат і сестра. У них багато спільного, але вони все ж різняться. Ці відмінності – їх особливі властивості, якими потрібно користуватися. Було б дивно знати про них і не застосовувати у вирішенні завдань.
Якщо продовжити аналогії і згадати ще одну фігуру – квадрат, то вона буде продовженням ромба і прямокутника. В цій фігурі об’єднані всі властивості і одного, і іншого.
Властивості ромба
Їх п’ять і вони перераховані нижче. Причому деякі з них повторюють властивості паралелограма, а якісь властиві тільки розглянутої фігурі.
- Ромб – це паралелограм, який прийняв особливу форму. З цього випливає, що його боки є попарно паралельними і рівними. Причому рівні вони непросто попарно, а всі. Як це було б у квадрата.
- Діагоналі цього чотирикутника перетинаються під кутом, який дорівнює 90?. Це зручно і багато в чому спрощує хід міркувань при вирішенні завдань.
- Інша властивість діагоналей: кожна з них ділиться точкою перетину на рівні відрізки.
- Лежать один навпроти одного кути у цієї фігури рівні.
- І остання властивість: діагоналі ромба збігаються з біссектрисами кутів.

Позначення, які прийняті в розглянутих формулах
В математиці належить вирішувати задачі з використанням загальних буквених виразів, які називаються формулами. Тема про площі не є винятком.
Для того щоб перейти до записів, які розкажуть, як знайти площу ромба, потрібно домовитися про букви, якими замінено всі числові значення елементів фігури.
Таблиця позначення елементів ромба
Назва елемента
Позначення
сторона ромба
а
велика діагональ
Д1
маленька діагональ
Д2
висота ромба
Н
гострий кут
А
тупий кут
В
радіус вписаного в ромб кола
загальноприйняті в математиці, позначення
площа фігури
Тепер прийшла пора написання формул.
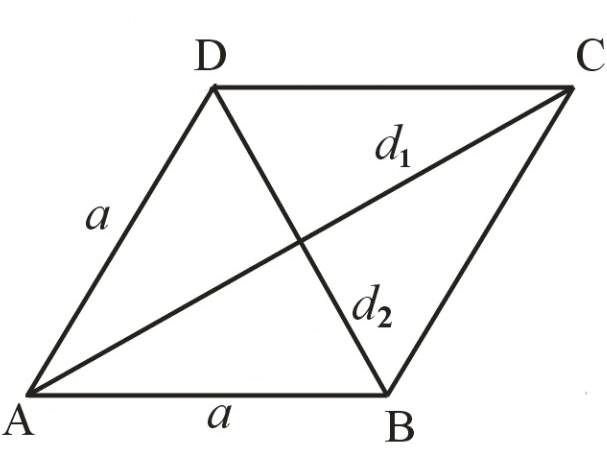
Серед даних задачі – діагоналі ромба
Правило стверджує, що для знаходження невідомої величини потрібно перемножити довжини діагоналей, а потім твір розділити навпіл. Результат ділення – це і є площа ромба через діагоналі.
Формула для цього випадку буде виглядати так:

Нехай ця формула буде йти під номером 1.
У задачі дано сторона ромба і його висота
Щоб обчислити площу, потрібно знайти добуток цих двох величин. Мабуть, це найбільш проста формула. Причому вона відома ще з теми про площу паралелограма. Там така формула вже вивчалася.
Математична запис:

Номер формули – 2.
Відомі сторона і гострий кут
В цьому випадку потрібно звести в квадрат величину сторони ромба. Потім знайти синус кута. І третьою дією обчислити добуток двох утворилися величин. Відповіддю буде площу ромба.
Літерне вираз:
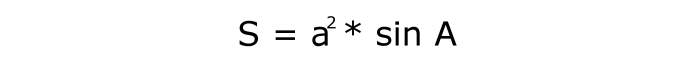
Його порядковий номер – 3.
Дані величини: радіус вписаного кола і гострий кут
Для обчислення площі ромба потрібно знайти квадрат радіуса і помножити його на 4. Визначити значення синуса кута. Потім розділити твір на другу величину.
Формула приймає такий вигляд:

Вона буде пронумерована цифрою 4.
У задачі фігурують сторона і радіус вписаного кола
Щоб визначити, як знайти площу ромба, потрібно обчислити добуток цих величин і числа 2.
Формула для цієї задачі буде виглядати так:
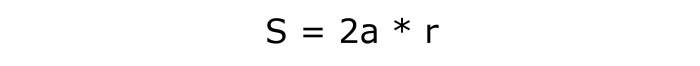
Її номер по порядку – 5.
Приклади можливих завдань
Завдання 1
Одна з діагоналей ромба дорівнює 8, а інша – 14 див. Потрібно знайти площу фігури і довжину її боку.

Рішення
Для знаходження першої величини потрібно формула 1, в якій Д1 = 8, Д2 = 14. Тоді площа обчислюється так: (8 * 14) / 2 = 56 (см2).
Діагоналі ділять ромб на 4 трикутника. Кожен з них обов’язково буде прямокутним. Цим треба скористатися, щоб визначити значення другої невідомої. Сторона ромба стане гіпотенузою трикутника, а катетами будуть половини діагоналей.
Тоді а2 = (Д1 /2)2 + (Д2 /2) 2. Після підстановки всіх значень виходить: а2= (8 / 2)2 + (14 / 2)2 = 16 + 49 = 65. Але це квадрат сторони. Значить, треба витягти квадратний корінь з 65. Тоді довжина сторони буде приблизно дорівнює 8,06 див.
Відповідь: площа 56 см2, а сторона 8,06 див.
Завдання 2
Сторона ромба має значення, рівне 5,5 дм, а його висота – 3,5 дм. Знайти площу фігури.
Рішення
Для того щоб знайти відповідь потрібна буде формула 2. У ній а = 5,5, Н = 3,5. Тоді, замінивши у формулі літери, числа, отримаємо, що шукана величина дорівнює 5,5 * 3,5 = 19,25 (дм2).
Відповідь: площа ромба дорівнює 19,25 дм2.
Завдання 3
Гострий кут біля деякого ромба дорівнює 60°, а його менша діагональ – 12 див. Потрібно обчислити його площу.
Рішення
Щоб отримати результат, потрібна буде формула під номером 3. В ній замість А буде 60, а значення а невідомо.
Для знаходження сторони ромба потрібно згадати теорему синусів. У прямокутному трикутнику а буде гіпотенузою, менший катет дорівнює половині діагоналі, а кут ділиться навпіл (відомо властивості, де згадується бісектриса).
Тоді сторона а буде дорівнює добутку катета на синус кута.
Катет потрібно обчислити як Д/2 = 12/2 = 6 (см). Синус(А/2) буде дорівнює його значенню для кута 30?, тобто 1/2.
Виконавши нескладні обчислення, отримаємо таке значення сторони ромба: а = 3 (см).
Тепер площа – це твір 32 і синуса 60?, тобто 9 * (?3)/2 = (9?3)/2 (см2).
Відповідь: шукана величина дорівнює (9?3)/2 см2.
Підсумки: все можливо
Тут були розглянуті деякі варіанти того, як знайти площу ромба. Якщо в задачі безпосередньо незрозуміло, яку формулу використовувати, то треба трохи подумати і спробувати пов’язати раніше вивчені теми. В інших темах обов’язково знайдеться підказка, яка допоможе зв’язати відомі величини з тими, що є у формулах. І завдання вирішиться. Головне – пам’ятати, що всі раніше вивчене можна і потрібно використовувати.
Крім запропонованих завдань, можливі і зворотні задачі, коли на площі фігури потрібно вирахувати значення будь-якого елемента ромба. Тоді потрібно скористатися тим рівнянням, яке найближче до умови. А потім перетворити формулу, залишивши в лівій частині рівності невідому величину.






