Види трикутників. Кути трикутника

Найпростіший багатокутник, який вивчається в школі — це трикутник. Він більш зрозумілий для учнів і зустрічає менше труднощів. Незважаючи на те, що існують різні види трикутників, у яких є особливі властивості.

Яка фігура називається трикутником?

Утворена трьома точками і відрізками. Перші називаються вершинами, другі — сторонами. Причому всі три відрізки повинні бути з’єднані, щоб між ними утворювалися кути. Звідси і назва фігури «трикутник».

Відмінності в назвах по кутах

Оскільки вони можуть бути гострими, тупими і прямими, то і види трикутників визначаються за цим назвам. Відповідно, груп таких фігур три.

• Перша. Якщо всі кути трикутника гострі, то він буде мати назву гострокутного. Все логічно.

• Друга. Один з кутів тупий, отже трикутник тупокутний. Простіше нікуди.

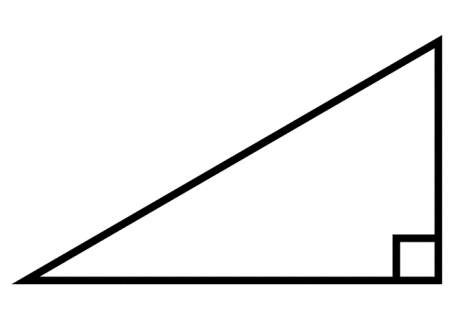
• Третя. Є кут, що дорівнює 90 градусам, який називається прямим. Трикутник стає прямокутним.

Відмінності в назвах по сторонам

Залежно від особливостей сторін виділяють такі види трикутників:

• загальний випадок — різнобічний, в якому всі сторони мають довільну довжину;

• рівнобедрений, у двох сторін якого є однакові числові значення;

• рівносторонній, довжини всіх його сторін однакові.

Якщо в завданні не вказано конкретний вид трикутника, то потрібно креслити довільний. У якого всі кути гострі, а сторони мають різну довжину.

Властивості, загальні для всіх трикутників

1. Якщо скласти всі кути трикутника, то вийде число, що дорівнює 180?. І неважливо, якого виду. Це правило діє завжди.
2. Числове значення будь-якої сторони трикутника менше, ніж складені разом дві інші. При цьому вона ж більше, ніж їх різниця.
3. Кожен зовнішній кут має значення, яке виходить при додаванні двох внутрішніх, не суміжних з ним. Причому він завжди більше, ніж суміжний з ним внутрішній.
4. Навпаки меншої сторони трикутника завжди лежить найменший кут. І навпаки, якщо сторона велика, то і кут буде найбільшим.

Ці властивості справедливі завжди, будь-які види трикутників ні розглядалися в задачах. Всі інші випливають з конкретних особливостей.

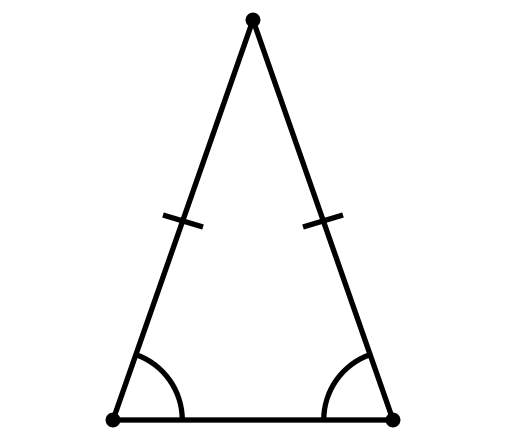
Властивості рівнобедреного трикутника

• Кути, що прилягають до основи, рівні.
• Висота, яка проведена до основи, є також медіаною та бісектрисою.
• Висоти, медіани і бісектриси, які побудовані до бічних сторін трикутника відповідно дорівнюють один одному.

Властивості рівностороннього трикутника

Якщо є така фігура, то будуть вірні всі властивості, описані трохи вище. Тому що рівносторонній завжди буде рівнобедреним. Але не навпаки, рівнобедрений трикутник не обов’язково буде рівностороннім.

• Всі його кути дорівнюють один одному і мають значення 60?.
• Будь-яка медіана рівностороннього трикутника є його висотою і бісектрисою. Причому вони рівні один одному. Для визначення їх значень існує формула, яка складається з твору боку на квадратний корінь з 3, ділиться на 2.

Властивості прямокутного трикутника

• Два гострих кута дають в сумі значення в 90?.
• Довжина гіпотенузи завжди більше, ніж у будь-якого з катетів.
• Числове значення медіани, проведеної до гіпотенузі, дорівнює її половині.
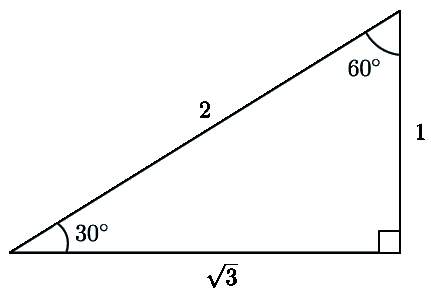
• Цим же значенням дорівнює катет, якщо він лежить навпроти кута в 30?.
• Висота, яка проведена з вершини зі значенням 90?, має певну математичну залежність від катетів: 1/н² = 1/² + 1/². Тут: а, у — катети, н — висота.

Завдання з різними видами трикутників

№1. Дано рівнобедрений трикутник. Його периметр відомий і дорівнює 90 див. Потрібно дізнатися його боку. В якості додаткової умови: бічна сторона підстави менше в 1,2 рази.

Рішення

Значення периметра безпосередньо залежить від тих величин, які потрібно знайти. Сума всіх трьох сторін і дасть 90 див. Тепер потрібно згадати ознака трикутника, яким він є рівнобедреним. Тобто дві сторони рівні. Можна скласти рівняння з двома невідомими: 2а + в = 90. Тут а — бічна сторона — підстава.

Настала черга додаткової умови. Слідуючи йому, виходить друге рівняння: у = 1,2 а. Можна виконати підстановку цього виразу в перше. Вийде: 2а + 1,2 = 90. Після перетворень: 3,2 а = 90. Звідси а = 28,125 (см). Тепер нескладно дізнатися підставу. Найкраще це зробити з другого умови: в = 1,2 * 28,125 = 33,75 (см).

Для перевірки можна скласти три значення: 28,125 * 2 + 33,75 = 90 (см). Все вірно.

Відповідь: сторони трикутника дорівнюють 28,125 см, 28,125 см, 33,75 див.

№2. Сторона рівностороннього трикутника дорівнює 12 див. Потрібно обчислити його висоту.

Рішення. Для пошуку відповіді досить повернутися до того моменту, де були описані властивості трикутника. Так вказана формула для знаходження висоти, медіани і бісектриси рівностороннього трикутника.

н = а * ?3 / 2, де н — висота, а — сторона.

Підстановка і обчислення дають такий результат: н = 6 ?3 (см).

Цю формулу запам’ятовувати необов’язково. Досить згадати, що висота ділить трикутник на два прямокутних. Причому вона виявляється катетом, а гіпотенуза в ньому — це сторона вихідного, другий катет — половина відомої сторони. Тепер потрібно записати теорему Піфагора і вивести формулу для висоти.

Відповідь: висота дорівнює 6 ?3 див.

№3. Дан МКР — трикутник, 90 градусів в якому становить кут К. Відомі боку МР і КР, вони дорівнюють відповідно 30 і 15 див. Потрібно дізнатися значення кута Р.

Рішення. Якщо зробити креслення, то стає ясно, що МР — гіпотенуза. Причому вона в два рази більше катета КР. Знову потрібно звернутися до властивостям. Одне з них якраз пов’язано з кутами. З нього зрозуміло, що кут КМР дорівнює 30?. Значить шуканий кут Р буде дорівнювати 60?. Це випливає з іншої властивості, яке стверджує, що сума двох гострих кутів повинна дорівнювати 90.

Відповідь: кут Р дорівнює 60°.

№4. Потрібно знайти всі кути рівнобедреного трикутника. Про нього відомо, що зовнішній кут від кута при основі дорівнює 110?.

Рішення. Оскільки дана тільки зовнішній кут, то цим і треба скористатися. Він утворює з внутрішнім кутом розгорнутий. Значить у сумі вони дадуть 180?. Тобто кут при основі трикутника дорівнює 70?. Так як він рівнобедрений, то другий кут має таке ж значення. Залишилося обчислити третій кут. По властивості, загальним для всіх трикутників, сума кутів дорівнює 180°. Значить, третій визначиться як 180? – 70? – 70? = 40?.

Відповідь: кути рівні 70?, 70?, 40?.

№5. Відомо, що в равнобедренном трикутнику кут, що лежить навпроти основи, дорівнює 90?. На підставі відзначена точка. Відрізок, що з’єднує її з прямим кутом, ділить його у відношенні 1 до 4. Потрібно дізнатися все кути меншого трикутника.

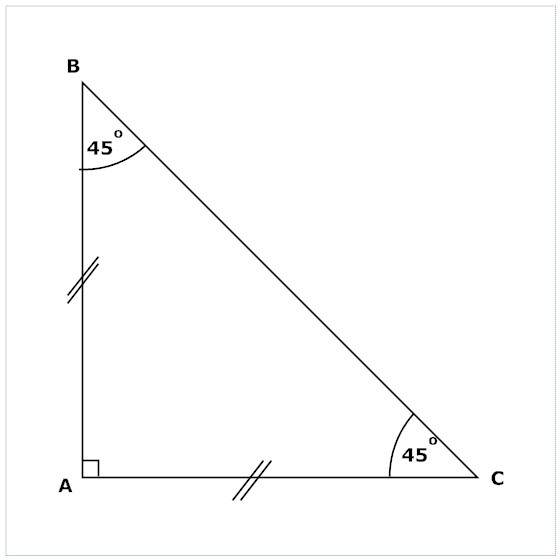
Рішення. Один з кутів можна визначити відразу. Оскільки трикутник і прямокутний рівнобедрений, то ті, що лежать біля його основи, 45?, тобто за 90?/2.

Другий з них допоможе знайти відоме в умові ставлення. Оскільки воно дорівнює 1 до 4, частин, на які він поділяється виходить всього 5. Значить, щоб дізнатися менший кут трикутника потрібно 90?/5 = 18с. Залишилося дізнатися третій. Для цього з 180? (суми всіх кутів трикутника) треба відняти 45? і 18?. Нескладні обчислення, і вийде: 117?.

Відповідь: 18?, 45?, 117?