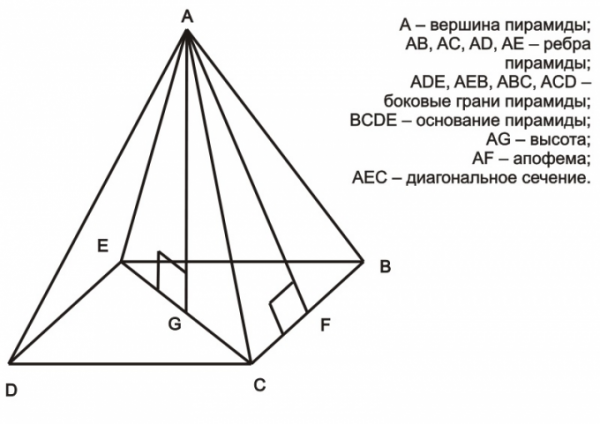
Під пірамідою розуміється одна з різновидів багатогранників, який утворений з лежачого в основі багатокутників і трикутників, які є його гранями й об’єднуються в одній точці – вершині піраміди. Знайти площу бічної поверхні піраміди не змусить особливих труднощів.
Інструкція
1. Насамперед, варто зрозуміти, що бічна поверхня піраміди представлена кількома трикутниками, площі яких можна знайти з допомогою різних формул, в залежності від відомих даних:
S = (a*h)/2, де h – висота, опущена на бік a;
S = a*b*sin?, де a, b – сторони трикутника, а ? – кут між цими сторонами;
S = (r*(a + b + c))/2, де a, b, c – сторони трикутника, а r – радіус вписаного в цей трикутник кола;
S = (a*b*c)/4*R, де R – радіус описаної навколо кола трикутника;
S = (a*b)/2 = r2 + 2*r*R (якщо трикутник – прямокутний);
S = S = (a2*?3)/4 (якщо трикутник рівносторонній).
Насправді, це лише основні з відомих формул для знаходження площі трикутника.
2. Розрахувавши за допомогою наведених вище формул площі всіх трикутників, що є гранями піраміди, можна приступити до обчислення площі бічної поверхні даної піраміди. Робиться це дуже просто: необхідно скласти площі всіх трикутників, що утворюють бічну поверхню піраміди. Формули це можна виразити так:
Ѕп = ?Si, де Ѕп – площа бічної поверхні піраміди, Si – площа i-го трикутника, яка є частиною її бічній поверхні.
3. Для більшої ясності можна розглянути невеликий приклад: дана правильна піраміда, бічні грані якої утворені рівносторонніми трикутниках, а в основі її лежить квадрат. Довжина ребра даної піраміди складає 17 див. Потрібно знайти площу бічної поверхні даної піраміди.
Рішення: відома довжина ребра даної піраміди, відомо, що межі її – рівносторонні трикутники. Таким чином, можна сказати, що всі сторони всіх трикутників бічній поверхні дорівнюють 17 див. Тому для того, щоб розрахувати площа будь-якого з цих трикутників, потрібно застосувати формулу:
S = (172*?3)/4 = (289*1.732)/4 = 125.137 см2
Відомо, що в основі піраміди лежить квадрат. Таким чином, зрозуміло, що даних рівносторонніх трикутників чотири. Тоді площа бічної поверхні піраміди розраховується так:
125.137 см2 * 4 = 500.548 см2
Відповідь: площа бічної поверхні піраміди складає 500.548 см2
4. Спочатку обчислимо площу бічної поверхні піраміди. Під бічною поверхнею розуміється сума площ всіх бічних граней. Якщо ви маєте справу з правильною пірамідою (тобто такий, в основі якої лежить правильний багатокутник, а вершина проектується в центр цього багатокутника), то для обчислення всій бічній поверхні досить помножити периметр підстави (тобто суму довжин усіх сторін многокутника, що лежить в основі піраміди) на висоту бічної грані (інакше званої апофемой) та поділити отримане значення на 2: Ѕб=1/2P*h, де Ѕб – це площа бічної поверхні, P – периметр основи, h – висота бічної грані (апофема).
5. Якщо ж перед вами довільна піраміда, то доведеться окремо обчислювати площі всіх граней, а потім їх складати. Оскільки бічними гранями піраміди є трикутники, скористайтеся формулою площі трикутника: S=1/2b*h, де b – це підстава трикутника, а h – висота. Коли площі всіх граней обчислені, залишається лише скласти їх, щоб отримати площу бічної поверхні піраміди.
6. Потім необхідно обчислити площу основи піраміди. Вибір формули для розрахунку залежить від того, який багатокутник лежить в основі піраміда: правильний ( тобто такий, всі сторони якого мають однакову довжину) або неправильний. Площа правильного багатокутника можна обчислити, помноживши периметр на радіус вписаного в многокутник колу і поділивши отримане значення на 2: Sn=1/2P*r, де Sn – площа багатокутника, P – це периметр, а r – це радіус вписаного в многокутник колу.
7. Усічена піраміда – це многогранник, який утворюється пірамідою і її перетином, паралельним основи. Знайти площу бічної поверхні зрізаної піраміди зовсім нескладно. Її формула дуже проста: площа дорівнює добутку половини суми периметрів підстав за апофему. Розглянемо приклад розрахунку площі бічної поверхні зрізаної піраміди. Припустимо, дана правильна чотирикутна піраміда. Довжини основи дорівнюють b=5 см, c = 3 див. Апофема a = 4 див. Щоб знайти площу бічної поверхні піраміди, потрібно спочатку знайти периметр підстав. У великому підставі він буде дорівнює p1=4b=4*5=20 див. В меншому підставі формула буде такою: p2=4c=4*3=12 див. Отже, площа дорівнюватиме: s=1/2(20+12)*4=32/2*4=64 див.
8. Якщо в основі піраміди лежить неправильний багатокутник, для обчислення площі фігури спочатку потрібно буде розбити багатокутник на трикутники, обчислити площу кожного, а потім скласти. В інших же випадках, щоб знайти бічну поверхню піраміди, потрібно знайти площу кожної її бічної грані і скласти отримані результати. У деяких випадках задача знаходження бічної поверхні піраміди може бути полегшена. Якщо одна бічна грань перпендикулярна до основи або дві суміжні бічні грані перпендикулярні до основи, то основа піраміди вважається ортогональною проекцією частини її бічній поверхні, і вони пов’язані формулами.
9. Щоб завершити обчислення площі поверхні піраміди, складіть площі бічної поверхні і основи піраміди.
10. Піраміда – це многогранник, одна з граней якого (основа) – довільний многокутник, а решта граней (бічні) – трикутники, що мають спільну вершину. За кількістю кутів підстави піраміди бувають трикутні (тетраедр), чотирикутні і так далі.
11. Піраміда є многогранником, має підставу у вигляді багатокутника, а інші грані трикутниками із загальною вершиною. Апофемой називається висота бічної грані правильної піраміди, проведена з її вершини.






